Any high school physics textbook talks about Kepler’s Laws of planetary motion after it introduces Newton’s laws of motion and Newton’s law of gravity. It is mentioned that planets go around the sun following elliptical orbits, with the sun at one of the two focal points. This is Kepler’s first law. Two other laws, which are formulated by Kepler, are mentioned after that. It is also mentioned that Newton’s laws of motion, coupled with Newton’s law of gravity, can be used to derive the Kepler’s laws. However, if my memory serves me well, the derivation of Kepler’s laws from Newton’s laws is only done for a circular orbit as opposed to an elliptical orbit in the high school textbooks. The books probably mention that a circle is a special case of an ellipse and the mathematics is much simpler for circular motion than elliptical motion.
When I read about Kepler’s laws in those books during high school, I was probably too immature to ask the deeper questions. The stress of JEE preparation didn’t help much either in that regard. Every moment was valuable and should be utilized solving complicated problems, each with 10 pulleys and 15 inclined planes, since these problems appeared often in the JEE question paper. Speculating about the correct derivation of Kepler’s laws was considered just a waste of time back then.
However, I revisited Kepler’s Laws sometime during the early days of my doctoral research when I had more time and more maturity to ask the deeper questions. I realized that I mainly had two doubts:
- Assuming that the planet is going in a circle around the sun with an uniform velocity, it can be easily shown that such a motion is indeed supported by an attractive gravitational force applied by the sun on the earth. That was shown in the high school physics textbooks too. However, why does the planet start rotating around the sun in a circle in the first place? If the sun is static and say the planet is at a distance from the sun, an attractive gravitational force will just pull the planet into the sun. Only if we assume that the planet has started rotating around the sun, we can show that such a motion is supported, using Netwon’s laws of motion and Netwon’s law of gravity.
- How can we show that an elliptical orbit is also supported by the same Netwon’s laws? I tried to show it analytically, but the differential equation wasn’t easy to solve unlike the case of the circular orbit. Also, what determines whether the planet will follow an elliptical orbit or a circular orbit?
A friend in graduate school probably mentioned to me at that point that the initial condition determines the orbit taken by the planet. Whenever the planets broke apart from the sun or came from elsewhere into the solar system- whatever be the case- the speed at which it got introduced into the sun’s gravity field and its initial direction determine whether it will go around the sun in a circle or in an ellipse. Based on the initial condition, it may also fly off and never come back. While the idea seemed interesting and plausible, I didn’t get a chance to verify it for myself by reading a college textbook on classical mechanics. While I took several courses on quantum mechanics, statistical mechanics, electromagnetism and solid state physics during my PhD, I didn’t take a good course in classical mechanics. I probably should have taken one.
Recently, the prolonged home isolation during lockdown gave me the chance to watch the celebrated series on cosmology- “Cosmos: A Personal Voyage”, hosted by Carl Sagan in 1980, in its entirety. I also watched a few episodes of the next season of the series, hosted by Neil deGrasse Tyson in 2014. In Episode 3 of either series, the host emphasizes on the importance of Kepler’s Laws in the advent of not just cosmology but science in general. In the collaboration with Tycho Brahe, Johannes Kepler observed the motion of various planets in the solar system meticulously with the telescope. Kepler concluded that the planets move in elliptical orbits and not in circular orbits (Kepler’s 1st law). He also came up with mathematical laws to describe such motion (Kepler’s 2nd and 3rd laws). While Kepler’s laws were purely empirical, several years later, Isaac Newton came up with his own laws on motion of all particles in general and the gravitational force they apply on each other. Using these universal laws, Newton, along with Edmond Halley (after whom the comet which reappears on earth every 76 years is named), showed that the motion of all planets and even the comets can be shown to follow Kepler’s empirical laws. Both Sagan and Neil Tyson seem to agree that this derivation of Kepler’s laws from Netwon’s laws (Sagan doesn’t talk much about this derivation in the show but talks about it in the accompanying book) is the first giant step in the field of physics and cosmology. The derivation shows that simple laws that govern the motion of just about any two commonplace bodies on earth can be used to explain and predict the motion of celestial objects. Such is the universality of these Newton’s laws.
These episodes of the “Cosmos” series motivated me to look back at Kepler’s laws again during these lockdown days. I found that a college level classical mechanics textbook indeed derives Kepler’s elliptical orbits from Newton’s laws, but lots of other new concepts are used to get there. And several pages are exhausted in the process. But, I told myself that physics wise only Newton’s laws should be needed to get to Kepler’s laws. I realized that once the differential equations are written down for Newton’s laws, solving them analytically for elliptical orbits isn’t trivial. This is what I had observed during my PhD days as well. I assumed that all the other new concepts are introduced in the college level classical mechanics textbook to carry out the derivation completely analytically. But, I wanted to avoid this analytical method, knowing from experience that this kind of analytical techniques is indeed not generalizable. Unless one is a mathematical genius, it’s extremely hard to solve every new problem, which is non-trivial, analytically.
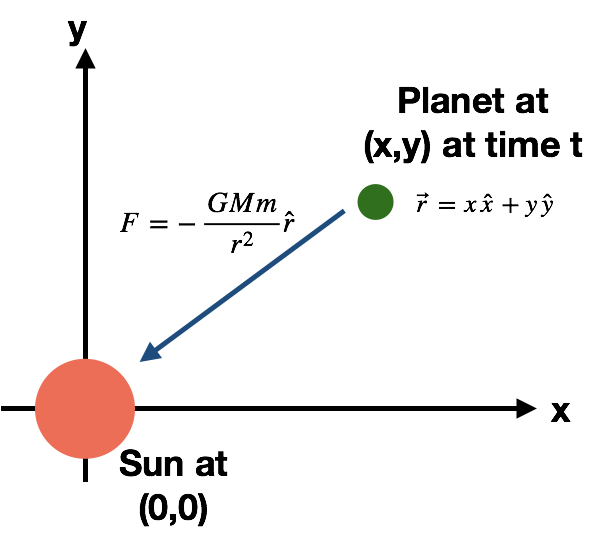
Hence, I decided to write the differential equations corresponding to the Netwon’s laws applied on the sun and the planet, and solve them numerically on a computer. Polar coordinates and all are not needed as a result and Cartesian coordinates (x,y) can be used as shown in the Figure 1 below:
The method followed:
The sun is at the origin (0,0) in Figure 1. The assumption is that though the planet pulls the sun due to gravity, the sun remains fixed. This holds true because the sun is much heavier than the planet. At any given time “t”, the planet is at position: (x,y). From Newton’s law of gravity, the force is experienced by the planet is given by:
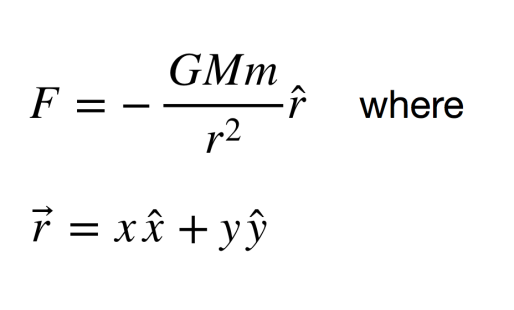
(as shown in Figure 1).
Using Newton’s 2nd law of motion (F=ma)- Newton’s 1st and 3rd laws of motion are special cases of this law- we can write:
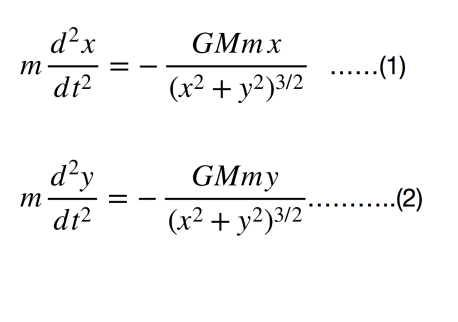
Now all I did was solving these two differential equations numerically. Initial conditions for position and velocity (x,y,dx/dt,dy/dt) are needed though. As can be seen next, these initial conditions determine the nature of the planet’s orbit and all other things, connected to the planet’s motion. For my initial condition, I always consider y=0, dx/dt=0, x>0 and dy/dt > 0. With respect to Figure 1, this means that at t=0, the planet is somewhere on the x axis, to the right of the sun, and the planet is moving orthogonal to the vector that connects the sun with the planet. By splitting the future time (t) into very small time steps and using the finite difference method, after every time step, the velocity (dx/dt, dy/dt) and the position (x,y) of the planet are calculated from equation (1) and (2). Thus, Kepler’s laws can also be obtained as I discuss below:
Kepler’s 1st law: The planet moves around the sun, following an elliptical orbit. The sun is at any one of the two focal points of the ellipse.
The following figures that I obtain (Figure 2,3 and 4) show that given that the initial position of the planet is the same (the sun is always at the origin), based on the initial velocity of the planet, it either takes a fairly circular trajectory (very low eccentricity value of the ellipse- we later show that for the case of the earth, the orbit is almost a circle) or a much more elliptical trajectory. For the nearly circular orbit (ellipticity =0.09) in Figure 2 (initial condition: x =1.5 A.U.,y=0,dx/dt=0, dy/dt= 25 km/s), the sun is at the center (two focal points of the ellipse overlap in this case). For the more elliptical trajectory (ellipticity= 0.55) in Figure 3, which is obtained when the initial velocity is higher (initial condition:x=1.5 A.U., y=0, dx/dt=0, dy/dt=30 km/s), the sun is at one of the two focal points. This is verified by calculating the eccentricity (e) from the length of semi-major axis (a) and the length of semi-minor axis (b) and then verifying that the distance between the sun and the planet initially (perihelion distance) is indeed a(1-e) as expected for an ellipse. When the initial velocity is even higher (35 km/s), the planet simply goes far away from the sun and never returns, as intuitively expected (Figure 4).
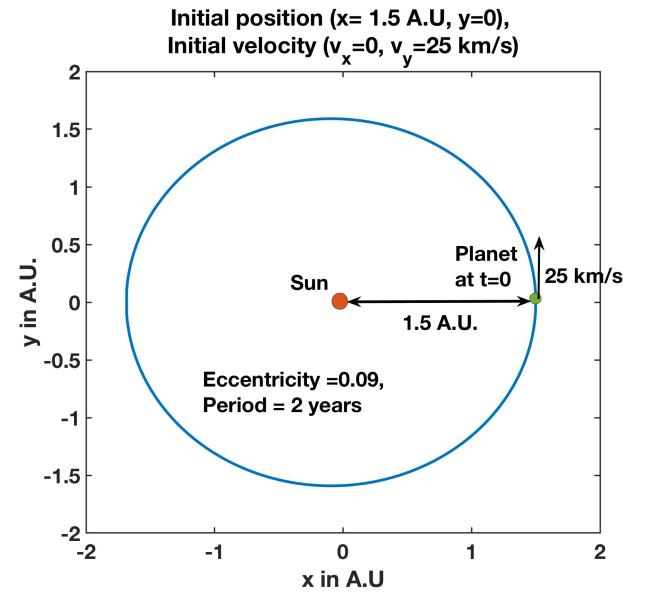
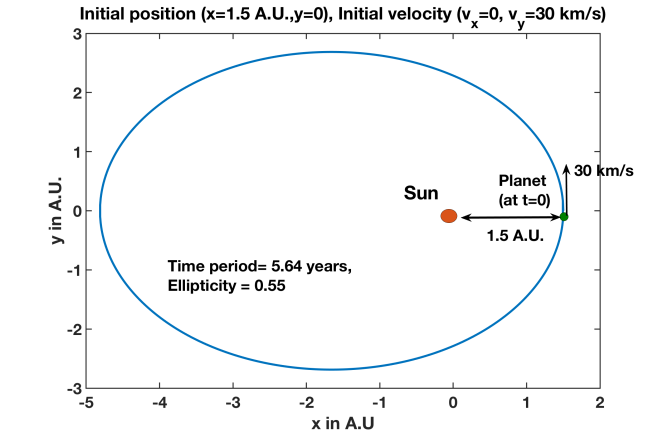
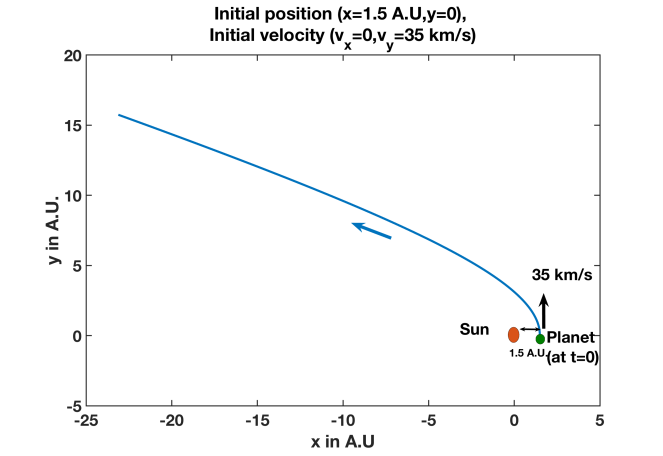
Thus Figure 2,3 and 4 not only show evidence for the Kepler’s first Law but also verify my friend’s claim that the initial condition of the planet determines its trajectory. Intuitively, when a planet has a very high velocity, it can simply avoid the gravitational pull of the sun and fly off. When the initial velocity is lower, the planet gets trapped by the gravitational field and keeps orbiting around the sun. However a certain magnitude of initial velocity, orthogonal to the vector connecting the sun and the planet (velocity in y direction in Figure 2,3 and 4), is needed for that to happen. In absence of that velocity, the planet will simply be drawn into the sun. Thus, both the doubts I had initially on this topic during my PhD days, as I had mentioned earlier, got resolved after doing these computations. Nevertheless, I carried out some more computations and generated some more plots to verify the other two laws, formulated by Kepler.
Kepler’s 2nd law: The planet sweeps out equal areas at equal times during its motion.
I calculated the area swept out by the planet per unit time (dA/dt) using the expression:
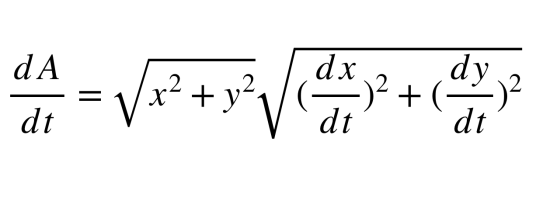
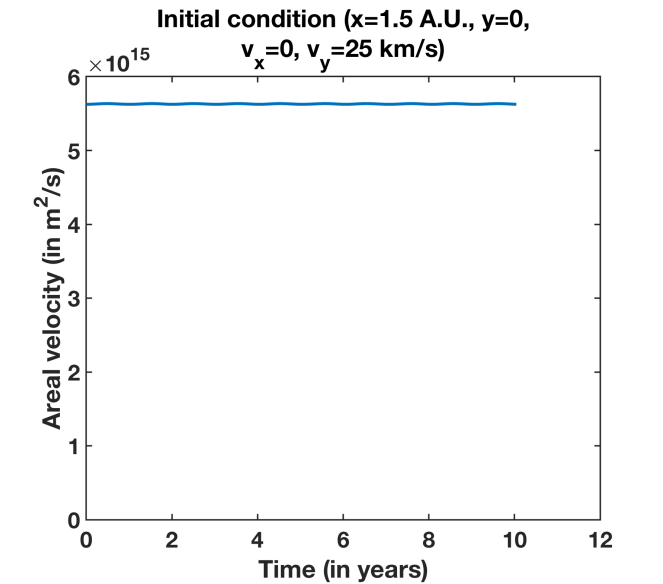
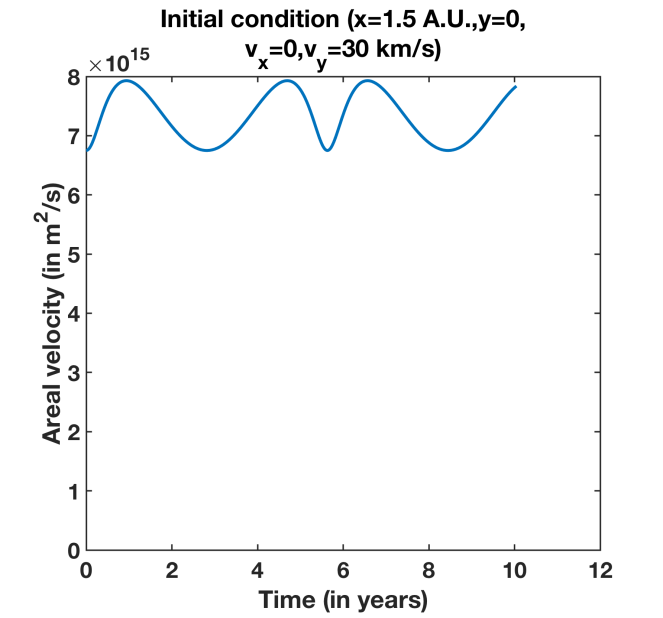
for all time instants (t) during the motion. Figure 5 shows the plot of dA/dt versus time (t) for the initial condition corresponding to Figure 2 (x =1.5 A.U.,y=0,dx/dt=0, dy/dt= 25 km/s). Figure 6 shows the plot of dA/dt versus time (t) for the initial condition corresponding to Figure 3 (x =1.5 A.U.,y=0,dx/dt=0, dy/dt= 30 km/s). In both cases, we see that the areal velocity is constant with respect to time, thus showing evidence for Kepler’s 2nd law.
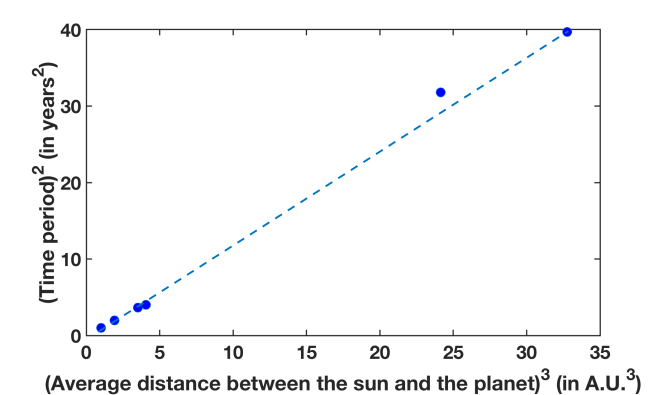
Kepler’s 3rd law: Square of the time period of the planet’s motion about the sun is proportional to the cube of the average distance of the planet from the sun.
For the cases corresponding to Figure 2 and Figure 3, the square of the time period is plotted against the cube of the average distance between sun and the planet in Figure 7 below. For several other initial conditions with different initial values of x and dy/dt (y=0, dx/dt=0 always), corresponding orbits are obtained and the square of time period is again plotted against the cube of the average distance between sun and the planet in Figure 7 below. As we can see from Figure 7, a straight line can indeed be passed through all the points. This shows evidence that Kepler’s third law is valid for planetary motion about the stars.
It is to be noted that in the case of all the laws, I have said that my computations show evidence for the Kepler’s laws, as opposed to saying that my computations prove the laws. This is because I think that in order to prove the laws, analytical expressions are needed to be obtained. As I mentioned before, a college level classical mechanics textbook follows such an analytical method, but I do not follow the analytical method over here.
Comparison of the planetary trajectories computed here with actual astronomical observations:
I was particularly interested in matching the result of my computation with the actual motion observed for planetary/ celestial bodies. Two planets caught my interest. One was of course our earth. The second was Mars. This was because I learned from Episode 3 of “Cosmos- A Personal Voyage” that observation of the Mars’s orbit through the telescope made Kepler strongly doubt the prevalent idea that planetary orbits are circular. As he found out, Mars’s orbit is elliptical and not circular.
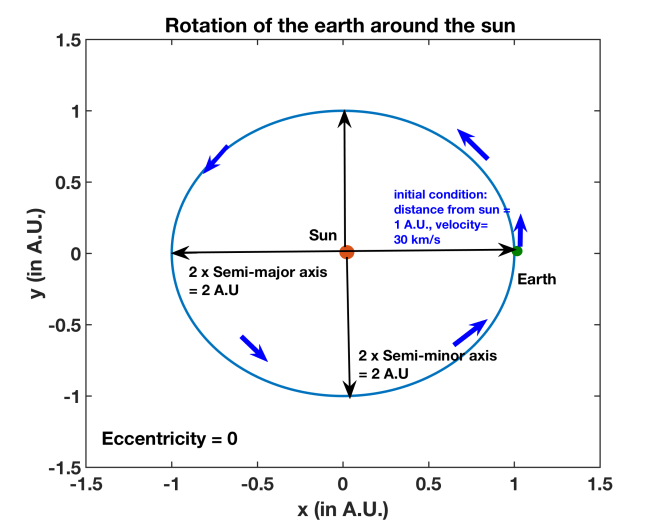
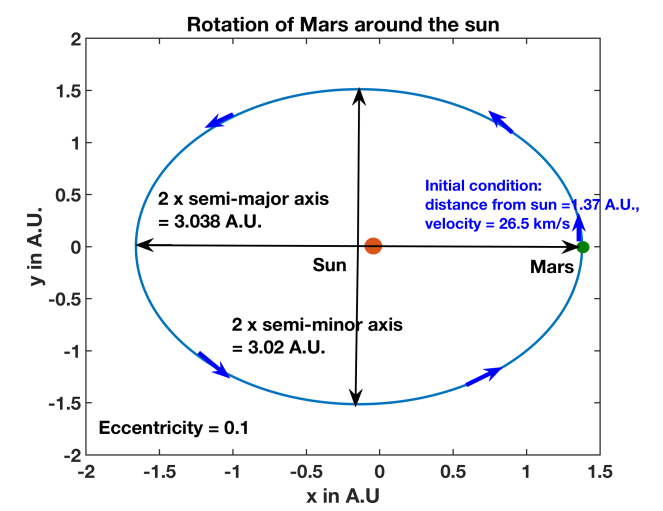
I gathered the following information: distance between earth and sun when they are closest/ perihelion distance (1 A.U.), velocity of earth at that point (30 km/s), distance between Mars and sun when they are closest/ perihelion distance (1.38 A.U.) and velocity of Mars at that point (26.5 km/s). I used the Wikipedia articles, related to the same, and associated research article- “Numerical expressions for precession formulae and mean elements for the Moon and planets”, Astronomy and Astrophysics, 282 (2): 663–683- for this purpose. I used these numbers as initial conditions in the equations (1) and (2) mentioned above, solved the equations numerically (as mentioned above) and obtained the trajectories of both the earth (Figure 8) and Mars (Figure 9). The eccentricity and time period (earth: 1 year, Mars: 1.9 years), obtained from my calculations, matched with that mentioned in the Wikipedia articles and the associated research article. While earth follows a circular orbit (eccentricity= 0), Mars follows a slightly elliptical orbit (eccentricity= 0.1).
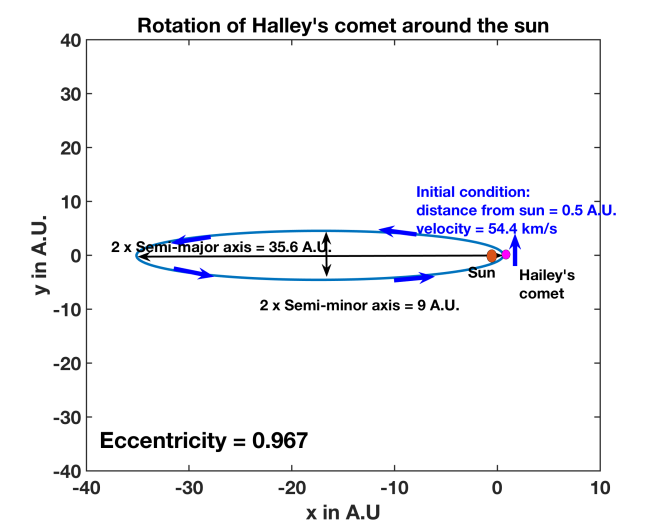
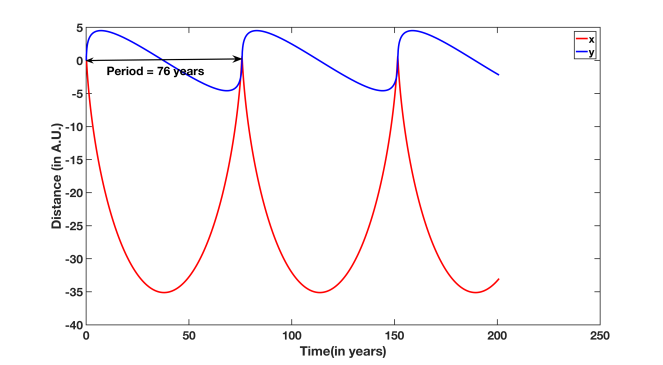
The third body that fascinated me was the Halley’s comet. Neil deGrasse Tyson spent a large proportion of Episode 3 of “Cosmos- A Spacetime Odyssey” discussing how Halley worked with Newton to predict the elliptical orbit of the Hailey’s comet. The geometry of the comet’s trajectory fascinated me as much as the tale, connected to its discovery. The sun is at one of the two focal points of the highly eccentric ellipse, which Halley’s comet follows. Hence, when the comet comes very close to the sun (perihelion), it moves very fast. And when it is far away from the sun (aphelion), it moves very slow (Kepler’s second law: aerial velocity remains constant). The period of the orbit is 76 years. Thus, Halley’s comet shows up near the sun and the earth every 76 years, moves very fast and disappears.
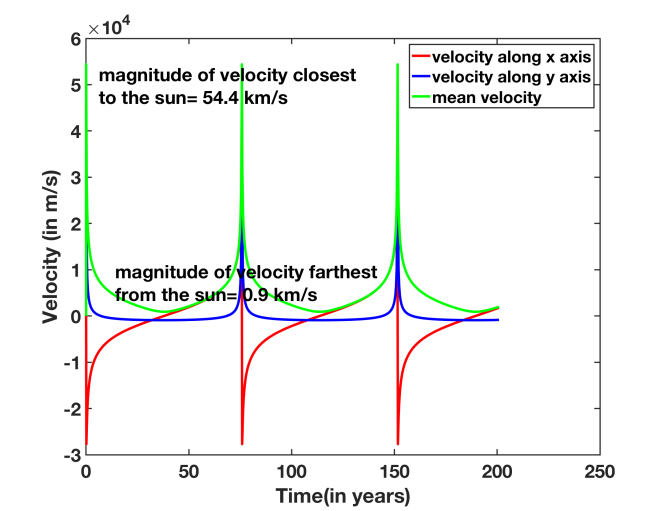
Following the same method that I followed for computing the orbit of earth and Mars, I could compute the much more elliptical orbit that Halley’s comet follows. I even got the eccentricity and the time period of the orbit to match with numbers reported in the Wikipedia article on Halley’s comet and associated research data in the Jet Propulsion Laboratory’s database(https://ssd.jpl.nasa.gov/sbdb.cgi?sstr=1P). Both the eccentricity (0.967) and the time period (76 years) of Halley’s comet’s orbit turned out to be much higher than that of the earth and Mars, as anticipated (Figure 10, Figure 11). When the comet is the farthest from the sun, its velocity is as low as 0.9 km/s in my computation (Figure 12), which also matches with the actual number reported elsewhere (https://ui.adsabs.harvard.edu/abs/1982S%26W….21…21R/abstract). Of all the results I obtained in connection to this article, being able to predict this highly elliptical and mostly slow trajectory of Halley’s comet gave me the most delight- I must admit!
Further speculation:
Thus, I have been able to resolve most of the doubts I initially had, connected to Kepler’s Laws, through this computation. As it turns out, the initial condition (distance from the sun and the velocity) play a key role in determining the trajectory of the planet or the comet. That makes me speculate what are the odds of such a thing happening. The possibility is quite high that fragments broken from the sun, or objects coming from elsewhere, are introduced in the sun’s gravitational field with such a high velocity that they simply fly off. Or their initial velocities can be so low that they get pulled into the sun. Yet, there are nine distinct planets and other smaller bodies around the sun, like the Halley’s comet, which go around and around the sun in circles and ellipses. Most of the planets also have satellites, which go around the them following similar orbit. I also learned from “Comos: A Personal Voyage” that most stars in the Milky Way galaxy have about ten planets on an average. Thus, the odds that a broken fragment from a star goes around and around the star in an orbit aren’t significant, though they are quite low. Is there a formal method to calculate the odds? I don’t know at the moment. May be I shall look it up and think about it more. It can probably be the topic of another article in this series.
